 メソッドは自分自身を呼び出すことができます。Mainメソッドも例外ではありません。
メソッドは自分自身を呼び出すことができます。Mainメソッドも例外ではありません。
メソッドが自分自身を呼び出すことを再帰(的)呼び出し(recrusive call)といいます。
昔からCでは、この再帰呼び出しを行う例には、階乗の計算が取り上げられています。
C#でも、階乗を求めるプログラムを作ってみましょう。
その前に、「階乗って何?」という人のために階乗の説明をしておきます。
0または正のの整数nに対して、n * (n - 1) * (n - 2) *...* 2 * 1をnの階乗といいます。さて、nが0の時は困ってしまいますが、これは1と定義されています。記号ではn!と書きます。
どんな感じになるのでしょうか。
とりあえず階乗を求めるメソッドをint kai(int n)としておきます。 もし、nが1以下であれば、1を返して終了します。1より大きい場合は、n * kai(n - 1)を返してはどうでしょうか。自分自身を呼び出すたびにnは1ずつ減っていき、ついにはnが1になりますね。これで、n * (n - 1) * (n - 2) *...* 2 * 1の計算ができたことになるはずです。
// kaijo01.cs
using System;
class Kaijo
{
public int kai(int n)
{
if (n <= 1)
return 1;
else
return n * kai(n - 1);
}
}
class kaijo01
{
public static void Main()
{
Kaijo k = new Kaijo();
for (int i = 0; i < 10; i++)
Console.WriteLine("{0}! = {1}", i, k.kai(i));
}
}
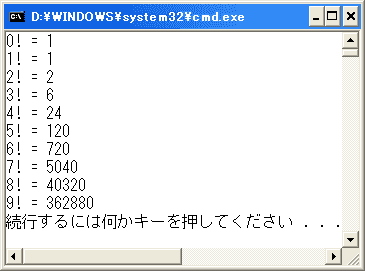
実行結果は次のようになります。

しかし、階乗の計算はわざわざ再帰呼び出しをしなくても、次のようにすれば求まりますね。
// kaijo02.cs
using System;
class Kaijo
{
public int calc(int n)
{
int seki = 1;
if (n == 0)
return 1;
for (int i = 1; i <= n; i++)
seki *= i;
return seki;
}
}
class kaijo02
{
public static void Main()
{
Kaijo kai = new Kaijo();
for (int i = 0; i < 10; i++)
Console.WriteLine("{0}! = {1}", i, kai.calc(i));
}
}
実行結果はkaijo01.csのものと全く同じです。では、似たようなことを加算でやってみましょう。
0以上の整数についてf(n)= 0 + 1 +...+nの計算をするプログラムです。 (これも、for文で簡単にできますがあえて再帰呼び出しで作ってみます。)
// kyusu01.cs
using System;
class Kyusu
{
public int calc(int n)
{
if (n == 0)
return 0;
else
return n + calc(n - 1);
}
}
class kyusu01
{
public static void Main()
{
Kyusu ks = new Kyusu();
for (int i = 0; i <= 20; i++)
Console.WriteLine("f({0, 2}) = {1, 3}", i, ks.calc(i));
}
}
実行結果は、次のようになります。
 再帰呼び出しを行うメソッドでは、引数が有る条件になったら、再帰をやめなくてはいけません。そうしないと、永久に自分自身を呼び出し続けることになり、スタックを使い切ってしまいますね。
再帰呼び出しを行うメソッドでは、引数が有る条件になったら、再帰をやめなくてはいけません。そうしないと、永久に自分自身を呼び出し続けることになり、スタックを使い切ってしまいますね。
Update 03/Sep/2006 By Y.Kumei